Navigation
Sidebar
Table of Contents
Algorithm Implementation of Power for Model 8 Conditional Processes
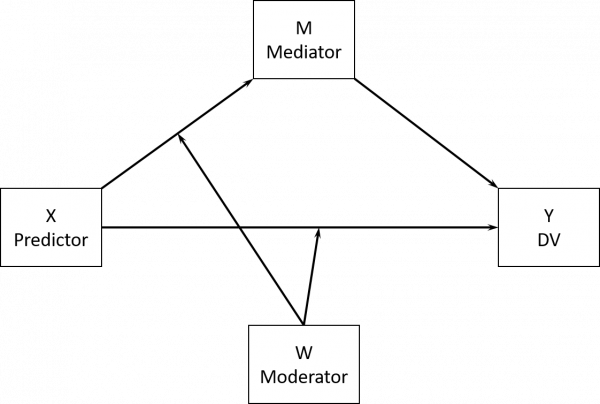
Mediation
X is the predictor and Y is the dependent variable . Variable X’s effect on a second variable Y is said to be mediated by a third variable M if X causally influences M and M in turn causally influences Y, and then M is the mediator in the model.
Moderation
A variable’s effect on another is moderated if its size depends on a third variable-a moderator. W is the moderator in the model.
The conditional indirect process model:
$$ M=i_{M}+a_{1}X+a_{2}W+a_{3}XW $$
XW is the product of X and W. If W moderates X’s effect on M, it is said that X and W interact in their influence on M. Equation above can be written in an equivalent form as
$$ M=i_{M}+(a_{1}+a_{3}W)X+a_{2}W $$
which shows that X’s effect on M is a linear function of W.
The conditional direct model:
$$ Y=i_{Y}+c'X+b_{1}M+b_{2}W+b_{3}XW $$
It can be written as
$$ Y=i_{Y}+b_{1}M+(c'+b_{3}W)X+b_{2}W $$
In the model, Conditional indirect effect of X on Y through M is $(a_{1}+a_{3}W)b_{1}$, Conditional direct effect of X on Y is $(c'+b_{3}W)$
In the power analysis, we use Monte Carlo simulation by assuming all variables are normally distributed. We require the input of the correlations between $X, W, M, XW, Y$. Based on the correlation matrix, $R$ sets of data are randomly generated from a multivariate normal distribution. For each set of data, least squares regression is used to get the parameter estimates and the associated test of significance.
The result of Power for Conditional Indirect Effect (On Mediator) and Conditional Indirect Effect (On DV) is computed by the following formulas:
$$ \begin{align*} \mathrm{JSa}&=\frac{\text{times of }a_{1}\text{ and }b_{1}\text{ passes the test}}{R \text{ times of the simulation}} \\ \mathrm{JSb}&=\frac{\text{times of }b_{2}\text{ and }b_{1}\text{ passes the test}}{R \text{ times of the simulation}} \end{align*} $$
How to use
We developed a web app based on wp.modmed.m8 function in the WebPower package. The input of the web app include the following:
- Sample Size
- Significance Level(alpha): the default value is 0.05.
- Number of Simulations
- Regression coefficient of mediator (m) on predictor (x)
- Regression coefficient of outcome (y) on predictor (m)
- Regression coefficient of outcome (y) on mediator (x)
- Regression coefficient of mediator (m) on moderator (w)
- Regression coefficient of mediator (m) on the product (xw)
- Regression coefficient of mediator (y) on moderator (w)
- Regression coefficient of mediator (y) on the product (xw)
- Variance of predictor (x)
- Variance of moderator w
- Variance of error in first regression equation
- Variance of error in second regression equation
- Covariance between x and w
- Moderator value
- Method
References
- Chris Aberson (2021). pwr2ppl: Power Analyses for Common Designs (Power to the People). R package version 0.2.0. https://CRAN.R-project.org/package=pwr2ppl.
- Aberson, C. L. (2019). Applied power analysis for the behavioral sciences. Routledge.